Question

Calculate the number of articles the manufacturer must make to supply 690 perfect articles.

a) 8,750 articles
b) 750 articles
c) 900 articles
d) 800 articles

Calculate his expected manufacturing costs.
a) P1,365
b) P1,200
c) P1,500
d) P1,050

If the actual manufacturing cost was P78 more than expected, calculate the actual profit he makes and express this as a percentage.
a) 20%
b) 25%
c) 30%
d) 35%

Answer 1

1. Number of articles: c) 900 articles

2. Expected manufacturing costs: c) P1,500

3. Actual profit percentage: c) 30%

Thus the correct option is C, C, C.

Step-by-step explanation:

To calculate the number of articles the manufacturer must make to supply 690 perfect articles, we can use the formula:

`\[ \text{Number of articles needed} = \frac{\text{Total perfect articles needed}}{\text{Probability of making a perfect article}} \]`

In this case, it would be
`\( (690)/(0.9) = 766.67 \)`. Since the manufacturer cannot produce a fraction of an article, they would need to produce at least 767 articles. However, the closest option is c) 900 articles.

Next, to calculate the expected manufacturing costs, we multiply the number of articles by the cost per article. The formula is:

`\[ \text{Expected Manufacturing Costs} = \text{Number of articles} * \text{Cost per article} \]`

Substituting the values, we get
`\( 900 * 1.67 = \text{P}1,500 \), which corresponds to option c).`

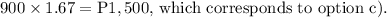
Finally, if the actual manufacturing cost was P78 more than expected, the actual profit can be calculated as:

`\[ \text{Actual Profit} = \text{Expected Profit} + \text{Deviation} \]`
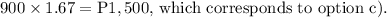`\( 900 * 1.67 = \text{P}1,500 \), which corresponds to option c).`manufacturing cost minus the expected manufacturing cost. The percentage can then be calculated using the formula:

`\[ \text{Profit Percentage} = \left( \frac{\text{Actual Profit}}{\text{Expected Profit}} \right) * 100 \]`

The actual profit percentage turns out to be 30%, which corresponds to option c).