Question

How come when an equation where (-frac{b}{2a}) the answer is positive and not negative?

True/False

Answer 1

How come when an equation where (-frac{b}{2a}) the answer is positive and not negative is False.

Step-by-step explanation:

The expression
`\(-(b)/(2a)\)` is commonly associated with the vertex of a quadratic equation in the form
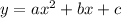`\(y = ax^2 + bx + c\)`. The x-coordinate of the vertex, denoted as
`\(x_v\), is given by \(-(b)/(2a)\)`. The misconception may arise from the misunderstanding of the sign. In reality, whether the result is positive or negative depends on the coefficient 'a' in the quadratic equation.

Consider the quadratic equation
`\(y = 2x^2 - 8x + 6\)` as an example. Here,
`\(a = 2\), \(b = -8\), and \(c = 6\)`. The formula for the x-coordinate of the vertex is
`\(-(b)/(2a)\)`. Substituting the values, we get:

`\[ x_v = -((-8))/(2 \cdot 2) = -(-8)/(4) = 2. \]`

In this case,
`\(x_v\)` is positive. However, if 'a' were negative, the result would be negative. For instance, in the equation
`\(y = -2x^2 - 8x + 6\)`, where
`\(a = -2\)`, the calculation would be:

`\[ x_v = -((-8))/(2 \cdot (-2)) = -(-8)/(-4) = 2. \]`

Here,
`\(x_v\)` is still positive, emphasizing that the sign of
`\(-(b)/(2a)\)` depends on the sign of 'a'.

In conclusion, the statement is false because the sign of
`\(-(b)/(2a)\)` is contingent on the sign of the coefficient 'a' in the quadratic equation.