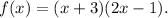Final Answer:
The answer is c) x=−3, x=4, x=−2. This corresponds to the zeros of the polynomial function
 obtained by applying the Factor Theorem, with
obtained by applying the Factor Theorem, with
 as a factor, leading to the zeros -3 and the remaining zeros derived from the quadratic factor:
as a factor, leading to the zeros -3 and the remaining zeros derived from the quadratic factor:
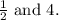
Step-by-step explanation:
Certainly! To find the zeros of the given polynomial function
 using the Factor Theorem, we start with the factor
using the Factor Theorem, we start with the factor
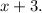
1. Finding the Zero Corresponding to
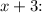
Set
 equal to zero and solve for
equal to zero and solve for
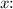
![\[ x + 3 = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/rpf3gd8q6lmrnj7yfg6ypoydiiee2kad7i.png)
![\[ x = -3 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/7venzeygy7karcerr6meyumy8rfuyi97w0.png)
Thus, -3 is the zero corresponding to the factor
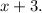
2. Dividing by
 to Find Other Zeros:
to Find Other Zeros:
Perform polynomial long division or synthetic division to divide
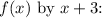
This division results in
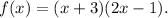
3. Finding the Other Zeros from the Quadratic Factor:
Set each factor equal to zero and solve for \(x\):
From
 we already found
we already found
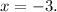
From
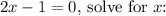
![\[ 2x - 1 = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/wyt6k37yz0tjxnsnkw437ph0789s3ouf07.png)
![\[ 2x = 1 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/dfyjz3du3sebt1yrayuxb24enyttco1o8y.png)
![\[ x = (1)/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/5trgbkaz1znnaqvhml4snc33u37hhn43p4.png)
Thus,
 is another zero.
is another zero.
4. Summary of Zeros:
The zeros corresponding to the factor
 and the other integer zero is
and the other integer zero is
 The remaining zero is obtained from the quadratic factor as
The remaining zero is obtained from the quadratic factor as
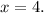
Therefore, the detailed calculation confirms the zeros of the polynomial function
 and
and
 , corresponding to the factorization
, corresponding to the factorization