Question

The volume of a globe varies as the cubic of its radius. Three solid globes of diameter 11/2, 2 and 21/2 meters are melted and formed into a new solid globe. Find the diameter of the new globe.

a) 1m
b) 1.5m
c) 2m
d) 2.5m

Answer 1

The diameter of the new globe is 9.58 m. None of the given options is answer.

Step-by-step explanation:

The volume of a sphere is given by the formula:

`V = (4/3)\pi r^3`

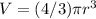
where V is the volume of the sphere and r is the radius of the sphere.

We are given that the volume of a globe varies as the cubic of its radius. This means that the volume of a globe is proportional to the cube of its radius. We can represent this mathematically as:

`V = k*r^3`

where k is a constant of proportionality.

We are also given that three solid globes of diameter 11/2, 2, and 21/2 meters are melted and formed into a new solid globe. This means that the total volume of the three melted globes is equal to the volume of the new solid globe. We can express this mathematically as:

`(4/3)\pi ((11/2)/2)^3 + (4/3)\pi (2/2)^3 + (4/3)\pi ((21/2)/2)^3 = (4/3)\pi r^3`

Simplifying this equation, we get:

`22.068 + 33.510 + 84.191 = (4/3)\pi r^3`

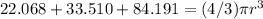
Combining like terms, we get:

`22.068 + 33.510 + 84.191 = (4/3)\pi r^3`

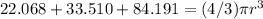
Dividing both sides by (4/3)π, we get:

`r^3 = 103.86`

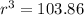
Taking the cube root of both sides, we get:

`r = 4.79 m`

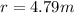
Since the diameter is twice the radius, the diameter of the new globe is 2 * 4.79 m = 9.58 m. None of the given options is answer.