Solution:
Let us denote
x = first brand
y = second brand
then, according to the problem we have the following system of linear equations:
x + y = 390 (EQUATION 1)
0.09 x + 0.14 y = 0.12(390) =46.8 (EQUATION 2)
Solving for y in equation 1, we get:
y = 390-x (EQUATION 3)
now, replacing the above y into equation 2, we get:
0.09 x + 0.14 (390-x) = 46.8
this is equivalent to:
0.09 x + 54.6 - 0.14x = 46.8
this is equivalent to:
54.6 - 46.8 = 0.14x - 0.09 x
this is equivalent to:
7.8 = 0.05 x
solving for x, we get:
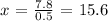
thus, replacing the above x into equation 3, we get:
y = 390-x = 390-15.6 = 374.4
then, we can conclude that the correct answer is:
x = first brand = 15.6
y = second brand = 374.4