Question

a chef is going to use a mixture of two brands of Italian dressing the first brand contains 9% vinegar in the second bracket a 14% vinegar the chef wants to make 390 mL of dressing that is 12% vinegar how much of each brand should she use

Answer 1

Solution:

Let us denote

x = first brand

y = second brand

then, according to the problem we have the following system of linear equations:

x + y = 390 (EQUATION 1)

0.09 x + 0.14 y = 0.12(390) =46.8 (EQUATION 2)

Solving for y in equation 1, we get:

y = 390-x (EQUATION 3)

now, replacing the above y into equation 2, we get:

0.09 x + 0.14 (390-x) = 46.8

this is equivalent to:

0.09 x + 54.6 - 0.14x = 46.8

this is equivalent to:

54.6 - 46.8 = 0.14x - 0.09 x

this is equivalent to:

7.8 = 0.05 x

solving for x, we get:

`x\text{ = }(7.8)/(0.5)\text{ = 15.6}`

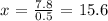
thus, replacing the above x into equation 3, we get:

y = 390-x = 390-15.6 = 374.4

then, we can conclude that the correct answer is:

x = first brand = 15.6

y = second brand = 374.4