Given that the cost of an item increases by 2.5% each year.
Suppose that a jacket cost $100 in the year 2017.
Here,
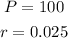
Suppose after n years, the cost of the jacket will be $600.
Then,
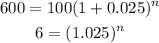
Taking logarithm of both sides,

By rounding to the nearest year, after 73 years the cost of the jacket will be $600.