Final answer:
To calculate the time for the automobile to overtake the truck, we use equations of motion with the truck's acceleration at 2.10 m/s² and the automobile's acceleration at 3.40 m/s². Setting the equal displacement for the point of overtaking and solving the equations shows that the automobile overtakes the truck in 9.81 seconds. So, the correct answer for t, which is option (b), 9.81 seconds
Step-by-step explanation:
1. Equations of Motion:
We will use the equations of motion for uniformly accelerated linear movement. The displacement for uniformly accelerated motion is given by
 , where u is the initial velocity (which is 0 since both start from rest), a is the acceleration, and t is the time.
, where u is the initial velocity (which is 0 since both start from rest), a is the acceleration, and t is the time.
2. Truck's Displacement:
The displacement
 for the truck is given by:
for the truck is given by:
![\[ s_t = (1)/(2) a_t t_t^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/pe4o5g3fu6akujxq56vaiisnc89iln3sn4.png)
3. Automobile's Displacement:
The displacement
 for the automobile is given by:
for the automobile is given by:
![\[ s_a = (1)/(2) a_a t_a^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/tlzczl3g77uhn0s0i0vopossmzx1xeuzn3.png)
4. Setting Displacements Equal:
Since the automobile overtakes the truck, the displacements are equal when the overtaking occurs. Thus, we have:
![\[ (1)/(2) a_t t_t^2 = (1)/(2) a_a t_a^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/lmlmliizb2qxz588p8xm5lrmb27hgibvph.png)
5. Given Values:
Given that the truck has moved
 when the automobile overtakes it, we set
when the automobile overtakes it, we set
 and solve for
and solve for
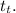
6. Calculations:
![\[ 40.0 = (1)/(2) * 2.10 * t_t^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/o4n02sqmua9r4fql93oril2miznhspp1fi.png)
7. Solving for
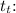
![\[ t_t = \sqrt{(2 * 40.0)/(2.10)} \]](https://img.qammunity.org/2024/formulas/physics/high-school/yeb1k3g0kdry4oz0h6kit9awkyhzyfwvi5.png)
8. Result:
After calculating, we find

Therefore, the correct answer for the time it takes for the automobile to overtake the truck is approximately
 (option b).
(option b).