Question

I need help with my homewrok PLEASE CHECK WORK number 5

Answer 1

Step-by-step explanation

So we must decide which of the four options best models the set of data. First of all it's important to notice that two of the options are linear models (B and C) and the other two are exponential models (A and D). Linear models are preferred when the diference between y-values remains almost constant. For example, the y-value difference (in this case the y-values are numbers of bacteria) between day 0 and day 1 is 228-137=91. Between day 4 and 5 is 1747-1050=697. And between day 2 and 3 is 631-379=252.

As you can see this difference varies considerably which means that a linear model is not a good fit so we can discard options B and C.

We have to decide between A and D. What we can do is evaluate the number of bacteria given by their equations for x=0, 1, 2, 3, 4 and 5 and compare the results with the table. The equation in A is:

`B=137(0.59)^(2.37x)`

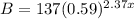
Then for all the x-values in the table we get:

`\begin{gathered} B=137(0.59)^(2.37\cdot0)=137 \\ B=137(0.59)^(2.37\cdot1)=39.23 \\ B=137(0.59)^(2.37\cdot2)=11.23 \\ B=137(0.59)^(2.37\cdot3)=3.22 \\ B=137(0.59)^(2.37\cdot4)=0.92 \\ B=137(0.59)^(2.37\cdot5)=0.26 \end{gathered}`

Now we do the same for option D. Its equation is:

`B=137(2.37)^(0.59\cdot x)`

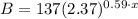
Then we get:

`\begin{gathered} B=137(2.37)^(0.59\cdot0)=137 \\ B=137(2.37)^(0.59\cdot1)=227.94 \\ B=137(2.37)^(0.59\cdot2)=379.25 \\ B=137(2.37)^(0.59\cdot3)=630.99 \\ B=137(2.37)^(0.59\cdot4)=1049.85 \\ B=137(2.37)^(0.59\cdot5)=1746.74 \end{gathered}`

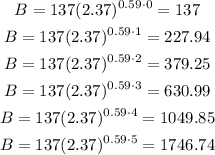
So for option A the numbers of bacteria are 137, 39.23, 11.23, 3.22, 0.92 and 0.26 whereas for option D we got 137, 227.94, 379.25, 630.99, 1049.85 and 1746.74. Comparing these two set of values to the one given by the table 137, 228, 379, 361, 1050 and 1747 is easy to note that those given by option D are much closer.

Answer

Then the answer is option D.