Question

Consider a triangle ABC like the one below. Suppose that B=103 degrees ,C=28 degrees , and b=52 . (The figure is not drawn to scale.) Solve the triangle. Round your answers to the nearest tenth. If there is more than one solution, use the button labeled "or".

Answer 1

Given:

Angle B = 103 degrees

Angle C = 28 degrees

Side b = 52 units

Find: measures of Angle A, side a, and side c.

Solution:

First, let's solve for the measure of Angle A.

Recall that the sum of the interior angles of a triangle is 180°. This means:

`AngleA+AngleB+AngleC=180\degree`

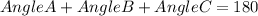
Since we already know the measure of angles B and C, we can subtract it from the total measure which is 180° to solve for the measure of Angle A.

`\begin{gathered} AngleA=180\degree-103\degree-28\degree \\ AngleA=49\degree \end{gathered}`

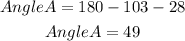
Therefore, the measure of Angle A is 49°.

Next, let's solve for the measure of side c using Sine Law.

`(sinB)/(b)=(sinC)/(c)`

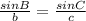
Let's plug into the equation above the value of B, C, and b.

`(sin103)/(52)=(sin28)/(c)`

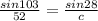
Then, solve for the value of c.

Cross multiply.

`(c)(sin103)=(52)(sin28)`

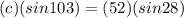
Divide both sides by sin 103.

`((c)(sin103))/((sin103))=((52)(sin28))/((sin103))\Rightarrow c=(52sin28)/(sin103)`

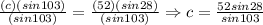
Evaluate the value of "c" using a calculator.

`c=25.0546\approx25.1`

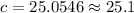
The measure of side c is approximately 25.1 units.

Lastly, to solve for the measure of side "a", we will still use sine Law.

`(sinA)/(a)=(sinB)/(b)`

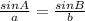
Let's plug into the equation above the value of A, B, and b.

`(sin49)/(a)=(sin103)/(52)`
`a=(52sin49)/(sin103)`
`a=40.277\approx40.3`

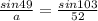
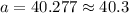
The measure of side a is approximately 40.3 units.