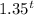Question

This table shows the number of reported cases of a disease in a

country. Instructors will check your answers for correctness.
Week
0
1
2
3
Size
12,000
16,200
21,870
29,525
4
Write an equation that would model this data. [a]
39,858

Answer 1

The equation that would model the data is f(t) = 12,000 ×
`1.35^t`

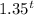
How do we find the equation that would model the data?

From week 0 to week 1 (16,200−12,000)/12,000 × 100 = 35

From week 1 to week 2: (21,870 - 16,200)/16,200 × 100 = 35

From week 2 to week 3 (29,525 - 21,870)/21,870 × 100 = 35

From week 3 to week 4 (39,858 - 29,525)/29,525 × 100 = 35

​

By calculating these, we can see if there's a consistent percentage increase, which would indicate exponential growth and allow us to model the growth with an exponential function of the form:

`f(t) = a * b^t`

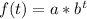
35% growth per week, which would be

1 + (35/100) = 1.35

The initial number of cases, a, is 12,000 at t = 0

The model equation is: f(t) = 12,000 ×
`1.35^t`