Question

Find all values of x that
make the triangles
congruent.

Answer 1

x = 5

Explanation:

Congruent triangles are the same size and shape, with corresponding angles and sides being equal in measure.

For the two provided triangles to be congruent, either ΔABC ≅ ΔDCB or ΔABC ≅ ΔDBC. So, this means that:

• 
  `\sf \overline{AB}\cong \overline{DC}\;\;and\;\;\overline{AC}\cong \overline{DB}`

• 
  `\sf \overline{AB}\cong \overline{DB}\;\;and\;\;\overline{AC}\cong \overline{DC}`

To find the value(s) of x that make the triangles congruent, we can set the expressions for the corresponding sides equal to each other and solve for x.

If ΔABC ≅ ΔDCB, then:

`\boxed{\begin{array}c\begin {aligned}\sf \overline{AB}&=\sf \overline{DC}\\3x-1&=4x-6\\3x-1-4x&=4x-6-4x\\-x-1&=-6\\-x-1+1&=-6+1\\-x&=-5\\x&=5\end{aligned}&\begin {aligned}\sf \overline{AC}&=\sf \overline{DB}\\x+7&=2x+2\\x+7-2x&=2x+2-2x\\-x+7&=2\\-x+7-7&=2-7\\-x&=-5\\x&=5\end{aligned}\end{array}}`

Therefore, ΔABC ≅ ΔDCB when x = 5.

If ΔABC ≅ ΔDBC, then:

`\boxed{\begin{array}c\begin {aligned}\sf \overline{AB}&=\sf \overline{DB}\\3x-1&=2x+2\\3x-1-2x&=2x+2-2x\\x-1&=2\\x-1+1&=2+1\\x&=3\end{aligned}&\begin {aligned}\sf \overline{AC}&=\sf \overline{DC}\\x+7&=4x-6\\x+7-4x&=4x-6-4x\\-3x+7&=-6\\-3x+7-7&=-6-7\\-3x&=-13\\x&=(13)/(3)\end{aligned}\end{array}}`

As the two values of x are not equal, ΔABC is not congruent to ΔDBC.

Therefore, the value of x that makes the triangles congruent is:

`\Large\boxed{\boxed{x=5}}`

Answer 2

x = 5

Explanation:

To make congruent triangle, the corresponding sides should be congruent.

Let's find all the value of x to make ∆ABC ≅ ∆DBC or ∆ ACB ≅ ∆DCB

For ∆ABC ≅ ∆DBC

AB ≅ BD and AC ≅ CD

For ACB ≅ ∆DCB

AB ≅ CD and AC ≅ BD

When

AB ≅ BD and AC ≅ CD

let's check congruent side

For ∆ABC ≅ ∆DBC

AB ≅ BD

Substitute value.

3x - 1 = 2x + 2

Subtract 2x on both sides:

3x - 1 - 2x = 2x + 2 - 2x

x -1 = 2

Add 1 on both sides:

x - 1 + 1 = 2 + 1

x = 3

let's check another congruent side

AC ≅ CD

Substitute value.

x + 7 = 4x - 6

Subtract x on both sides:

x + 7 -x = 4x - 6 - x

7 = 3x - 6

Add 6 on both sides:

7 + 6 = 3x - 6 + 6

13 = 3x

3x = 13

Divide both sides by 3.

`\sf (3x)/(3)=(13)/(3)`

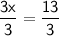
x = 4.3333

Since the value doesn't match.

So, x = 3 is not valid.

And

For ACB ≅ ∆DCB

When

AB ≅ CD and AC ≅ BD

let's check congruent side :

AB ≅ CD

Substitute value.

3x - 1 = 4x -6

Subtract 3x on both sides:

3x - 1 - 3x = 4x - 6 - 3x

-1 = -6 + x

Add 6 on both sides:

-1 + 6 = -6 + x + 6

5 = x

Let's check another one too

AC ≅ BD

Substitute value.

x + 7 = 2x + 2

Subtract x on both sides:

x + 7 - x = 2x + 2 - x

7 = x + 2

Subtract 2 on both sides:

7 -2 = x + 2 - 2

5 = x

x = 5

Since both values matched.

So, the only value of x is 5.