1 Answer

Nazira · Answer 1 · 2022-11-22T17:34:54+0000

Given:

A jar of coins has 8 pennies, 5 nickels, 1 dime, and 7 quarters.

To find:

The probability of drawing a quarter, replacing it, and drawing another quarter.

Solution:

A jar of coins has 8 pennies, 5 nickels, 1 dime, and 7 quarters.

Total number of coins = 8+5+1+7 = 21

Probability of getting a quarter is

$P(Quarter)=\frac{\text{Number of quarters}}{\text{Total number of coins}}$

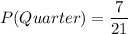
P(Quarter)=(7)/(21)

P(Quarter)=(1)/(3)

After drawing a quarter, we replaced it. So, the probability of getting quarter in second draw is the same and first one, .i.e.,
P(Quarter)=(1)/(3) .

The probability of drawing a quarter, replacing it, and drawing another quarter is

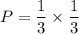
P=(1)/(3)* (1)/(3)

P=(1)/(9)

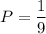
Therefore, the required probability is
.

Please log in or register to add a comment.