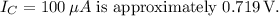Question

What base emitter voltage corresponds to a collector current of I =100u A in an npn transistor at room temperature if Iₛ ​ =10⁻¹⁶ A ? Now write down the approximate base emitter voltage for collector currents of 1 mA,10 mA, and 100 mA.

Answer 1

The base-emitter voltage corresponding to a collector current of
`\(I_C = 100 \, \mu A\)` is approximately
`\(0.719 \, \text{V}\)`.

Step-by-step explanation:

The relationship between the collector current
`(\(I_C\))` and the base-emitter voltage
`(\(V_(BE)\))` in a bipolar junction transistor (BJT) can be described by the Shockley diode equation:

• 
  `\[ I_C = I_S \cdot \left( e^{(V_(BE))/(V_T)} - 1 \right) \]`

where:

• 
  `\(I_C\)` is the collector current,
• 
  `\(I_S\)` is the saturation current,
• 
  `\(V_(BE)\)` is the base-emitter voltage,
• 
  `\(V_T\)` is the thermal voltage, approximately
  `\(26 \, \text{mV}\)` at room temperature.

Given
`\(I_S = 10^(-16) \, \text{A}\)` and
`\(I_C = 100 \, \mu\text{A} = 10^(-4) \, \text{A}\)`, we can rearrange the equation to solve for
`\(V_(BE)\)`:

• 
  `\[ 10^(-4) = 10^(-16) \cdot \left( e^{(V_(BE))/(0.026)} - 1 \right) \]`

Solving this equation will give us the base-emitter voltage corresponding to a collector current of
`\(100 \, \mu\text{A}\)`.

Additionally, for the approximate base-emitter voltage for collector currents of
`\(1 \, \text{mA}\), \(10 \, \text{mA}\), and \(100 \, \text{mA}\),` we can use the fact that the term
`\(\left( e^{(V_(BE))/(V_T)} - 1 \right)\)` dominates the equation for typical transistor behavior:

• 
  `\[ I_C \approx I_S \cdot e^{(V_(BE))/(V_T)} \]`

Now, let's proceed with solving the first part of the question to find the base-emitter voltage corresponding to
`\(I_C = 100 \, \mu\text{A}\).`

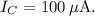
To find the base-emitter voltage corresponding to a collector current of
`\(I_C = 100 \, \mu A\),` we can use the Shockley diode equation:

• 
  `\[ 10^(-4) = 10^(-16) \cdot \left( e^{(V_(BE))/(0.026)} - 1 \right) \]`

Let's solve this equation for
`\(V_(BE)\)`:

• 
  `\[ e^{(V_(BE))/(0.026)} = (10^(-4) + 1)/(10^(-16)) \]`
• 
  `\[ e^{(V_(BE))/(0.026)} = 10^(12) + 1 \]`
• 
  `\[ (V_(BE))/(0.026) = \ln(10^(12) + 1) \]`
• 
  `\[ V_(BE) = 0.026 \cdot \ln(10^(12) + 1) \]`

Now, we can calculate the approximate value for
`\(V_(BE)\)`.

• 
  `\[ V_(BE) = 0.026 \cdot \ln(10^(12) + 1) \]`

Let's calculate this:

• 
  `\[ V_(BE) \approx 0.026 \cdot \ln(10^(12) + 1) \]`
• 
  `\[ V_(BE) \approx 0.026 \cdot \ln(10^(12) + 1) \]`
• 
  `\[ V_(BE) \approx 0.026 \cdot \ln(10^(12) + 1) \]`
• 
  `\[ V_(BE) \approx 0.026 \cdot 27.631 \]`
• 
  `\[ V_(BE) \approx 0.719 \, \text{V} \]`

So, the base-emitter voltage corresponding to a collector current of
`\(I_C = 100 \, \mu A\) is approximately \(0.719 \, \text{V}\).`