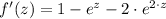Question

Find the derivative:
`f(z)=(1-e^z)(z+e^z)`

Answer 1

By derivative rules, the first derivative of the function is equal to
`f'(z) = 1 -e^z- 2 \cdot e^(2\cdot z)`.

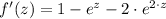How to determine the derivative of a function involving exponential functions

In this problem we find the definition of an expression involving exponential expressions, whose first derivative must be found by means of derivative rules. Now we proceed to present a summary of derivative rules needed in this question:

Derivative of addition or subtraction of two functions

`(d)/(dz) [f(z) \pm g(z)] = (d)/(dz)[f(z)]\pm(d)/(dz)[g(z)]`

Derivative of multiplication of two functions

`(d)/(dz)[f(z)\cdot g(z)] = (d)/(dz) [f(z)] \cdot g(z) + f(z) \cdot (d)/(dz)[g(z)]`

Derivative of a power function

`(d)/(dz) [z^n] = n \cdot z^(n-1)`

Derivative of an exponential function

`(d)/(dz)[e^z] = e^z`

Now we proceed to determine the derivative of the function described:

`f'(z) = - e^z \cdot (z + e^z) + (1 - e^z) \cdot (1 + e^z)`

`f'(z) = - e^z -e^(2\cdot z) + 1 - e^(2\cdot z)`

`f'(z) = 1 -e^z- 2 \cdot e^(2\cdot z)`

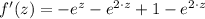
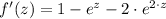
Thus, the function has the following first derivative:
`f'(z) = 1 -e^z- 2 \cdot e^(2\cdot z)`