Question

Part 4 (6 points)

A data scientist is asked to assess whether the development of kindergarten-aged children is
abnormally reduced in a Native American community where tailings from a uranium mine were
measured at dangerous levels for a 6-month period when the children were gestating in the
womb. The data scientist has little data to work with regarding the development of Native
American children in the region being assessed because a climate change induced flood
destroyed all the servers for the Bureau of Indian Affairs that housed this data. Additionally, the
communities in question are small. The data scientist selects a t-test as the test of significance
and chooses to show significance of at least p <.01. The mean height of children of the same age
as the children in question living in nearby Native American communities is 43 inches. In the
community exposed to uranium tailings, there are 16 children who were exposed to the toxin.
Their mean height is 39 inches with an SD of 3.5. Use Student's t-distribution on page A105 of
the textbook to determine if the children impacted by exposure to uranium tailings are
significantly shorter than children in nearby communities.

Answer 1

Using the Student's t-distribution, the conclusion is that the mean height of children in the community exposed to uranium tailings is significantly shorter than the mean height of children in nearby Native American communities at a significance level of .01.

The data scientist's test of significance = A t-test

Chosen significance level <01.

The mean height of children of the same age as the children in question living in nearby Native American communities = 43 inches

The number of children in the community exposed to uranium tailings, = 16 children

The mean height of these = 39 inches

The standard deviation = 3.5

Using the Student’s t-distribution on page A105 of the textbook, the formula for the t-test is:

`t = (\bar x - u) / (s / √(n) )`

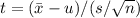
The sample mean =
`\bar x`

The population mean = μ

The sample standard deviation = s

The sample size = n

The null hypothesis (H₀): the mean height of children in the community exposed to uranium tailings is equal to the mean height of children in nearby Native American communities.

The alternative hypothesis (Hₐ): the mean height of children in the community exposed to uranium tailings is less than the mean height of children in nearby Native American communities.

The computation of the t-value is as follows:

t = (39 - 43) / (3.5 / √16) = -4.57

The critical value of t for a one-tailed test with 15 degrees of freedom and a significance level of .01 = -2.947.

Since the calculated t-value (-4.57) is less than the critical value (-2.947), we reject the null hypothesis and conclude that the mean height of children in the community exposed to uranium tailings is significantly shorter than the mean height of children in nearby Native American communities at a significance level of .01.