Question

Consider a uniform plane wave traveling in the air with its electric field given by E(x,t)-yI00 sin(2π x 10⁹ t-βz:)

V/m normally incident on the surface (z = 0) of a salty lake ( εᵣ= 78.8 and μᵣ= 1 at 1 GHz).
Assuming the lake to be perfectly flat and lossless (i.e., assume its conductivity is zero),
find the electric fields of the reflected and transmitted waves (i.e., Eᵣ(z,t) and Eₜ(z,t)

Answer 1

The electric fields of the reflected and transmitted waves can be found using the boundary conditions at the interface of the air and the salty lake. So,
`Et(z,t) = E(x,t) = y100 sin(2 \pi x 10^9 t- \beta z)V/m`

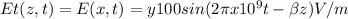
Step-by-step explanation:

The electric fields of the reflected and transmitted waves can be found using the boundary conditions at the interface of the air and the salty lake.

The electric field of the reflected wave,
`Er(z,t)`, can be found by taking the negative of the incident wave electric field,
`E(x,t)`, and replacing z with
`-z`.

So, in this case,
`Er(z,t) = -E(x,t) = -y100 sin(2\pi x 10^9 t-\beta z)V/m`.

The electric field of the transmitted wave,
`Et(z,t),` can be found by multiplying the incident wave electric field,
`E(x,t)`, by the transmission coefficient, which is given as 1 in this case since the conductivity of the lake is zero.

So,
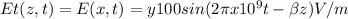`Et(z,t) = E(x,t) = y100 sin(2 \pi x 10^9 t- \beta z)V/m`.