Question

A parabola can be drawn given a focus of (11,5) and a directrix of x=3. What is the vertex, value of P, and direction of opening?

Answer 1

The vertex of the parabola is (3, 6.5). The value of P is approximately 8.13. The parabola opens upwards.

Step-by-step explanation:

The vertex, value of P, and direction of opening of a parabola can be determined using the given focus and directrix.

The vertex of the parabola is halfway between the focus and the directrix. Since the directrix is a vertical line with an equation of x=3, the x-coordinate of the vertex is 3. The y-coordinate of the vertex can be found by averaging the y-coordinate of the focus and the distance between the focus and the directrix. In this case, the y-coordinate of the focus is 5 and the distance between the focus and the directrix is 11-3=8, so the y-coordinate of the vertex is (5+8)/2=13/2 or 6.5.

The value of P is the distance between the focus and the vertex. Using the distance formula, we can calculate P as follows:

`P = sqrt((11-3)^2 + (5-6.5)^2)`

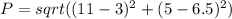
= sqrt(64 + 2.25)

= sqrt(66.25)

≈ 8.13.

Since the directrix is a vertical line, the parabola opens either upwards or downwards. In this case, since the focus is above the vertex, the parabola opens upwards.