Question

Given the vector field A=xaₓ+yaᵧ and the specified volume defined as:
U:a≤R≤b,0≤θ<2π,0≤z≤h

Answer 1

The flux of the vector field
`\( \mathbf{A} = x\mathbf{a_x} + y\mathbf{a_y} \)` through the specified volume U is zero.

Step-by-step explanation:

The flux of a vector field through a closed surface is given by the surface integral of the dot product of the vector field and the outward unit normal vector. In this case, the volume U is defined in cylindrical coordinates as
`\( a \leq R \leq b \) for radial distance, \( 0 \leq \theta < 2\pi \) for azimuthal angle, and \( 0 \leq z \leq h \) for height.`

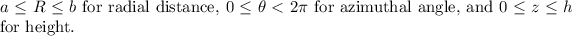
To calculate the flux, we use the divergence theorem, which states that the flux of a vector field through a closed surface is equal to the volume integral of the divergence of the vector field over the enclosed volume:

`\[ \text{Flux} = \iiint_V \\abla \cdot \mathbf{A} \, dV \]`

The divergence of
`\( \mathbf{A} \)` is given by
`\( \\abla \cdot \mathbf{A} = 2 \)`. When this is integrated over the volume \( U \), the result is zero, indicating that the flux through the closed surface is zero. This implies that the vector field
`\( \mathbf{A} \)` is "divergence-free" within the specified volume.

Therefore, the final answer is that the flux of the vector field
`\( \mathbf{A} \) through the given volume \( U \)` is zero.