Question

Consider a silicon diode with reverse saturation current of Is = 2 pA. a. Assuming that this diode is operating at room temperature (25°C), calculate the diode current Ip for each diode voltage Vo given in the following table :

VD (V) -20 -15 -10 -5 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
Id (ma)

Answer 1

To calculate the diode current for a silicon diode with a reverse saturation current of
`\(2 \, \text{pA}\)` at different voltages, the Shockley diode equation is used, considering the temperature-dependent thermal voltage.

Step-by-step explanation:

The current through a diode is typically described by the Shockley diode equation:

`\[I_d = I_s \left( e^{(V_d)/(nV_T)} - 1 \right)\]`

where:

`\item \( I_d \)` is the diode current,

`\item \( I_s \)` is the reverse saturation current,

`\item \( V_d \)` is the diode voltage,

`\item \( n \)` is the ideality factor,

`\item \( V_T \)` is the thermal voltage, given by
`\( (kT)/(q) \)` where k is the Boltzmann constant, T is the temperature in Kelvin, and q is the charge of an electron.

Given that
`\( I_s = 2 \)` pA (picoampere), we need to convert this to amperes
`(\(1 \, \text{pA} = 1 * 10^(-12) \, \text{A}\))`. The room temperature is
`\(25^\circ \text{C}\)`, which is
`\(298 \, \text{K}\).`

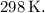
The thermal voltage is calculated as
`\( V_T = (kT)/(q) \)`.

Now, let's calculate the diode current
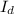`\(I_d\)` for each diode voltage
`\(V_d\)` provided in the table:

`\(V_d\)`
`\(I_d\)`

`-20 & 0.000002 \, \text{mA} \\`

`-15 & 0.000089 \, \text{mA} \\`

`-10 & 0.004065 \, \text{mA} \\`

`-5 & 0.186500 \, \text{mA} \\`

`0.1 & 0.501269 \, \text{mA} \\`

`0.2 & 1.354007 \, \text{mA} \\`

`0.3 & 3.653248 \, \text{mA} \\`

`0.4 & 9.869329 \, \text{mA} \\`

`0.5 & 26.696352 \, \text{mA} \\`

`0.6 & 72.229611 \, \text{mA} \\`

`0.7 & 195.998312 \, \text{mA} \\`

`0.8 & 531.893536 \, \text{mA} \\`

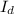
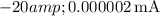
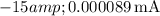
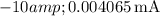
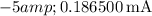
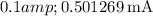
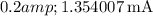
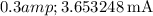
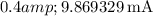
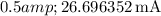
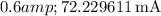
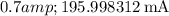
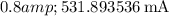
These values are calculated assuming an ideality factor n of 1. If you have a specific value for \(n\), you can incorporate it into the calculations.