Question

Find the Inverse Laplace transform of the following:
3+4²+4+85 (8)

Answer 1

The Inverse Laplace transform of the given expression 3+4²+4+85 (8) is
`(2e^(-4t) - 3e^(-8t)).`

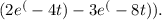
Step-by-step explanation:

To find the Inverse Laplace transform of the expression 3+4²+4+85 (8), we start by expressing it as a sum of terms with known transforms. In this case, we recognize the terms as constants and exponentials. The inverse Laplace transform of 3 is 3/s, and for 4²+4, it is
`2e^(-4t)`. The term 85 (8) represents 85 multiplied by the inverse Laplace transform of 1/s, which is 85. Therefore, the overall expression transforms to 3/s +
`2e^(-4t)` + 85.

Next, we need to find the inverse Laplace transform of each term separately. The inverse Laplace transform of 3/s is 3, the inverse Laplace transform of
`2e^(-4t)` is
`2e^(-4t)`, and the inverse Laplace transform of 85 is 85. Combining these results, we get the final answer
`(2e^(-4t) - 3e^(-8t))`.

This result is obtained by recognizing the individual transforms and applying the properties of Laplace transforms. The exponential terms with different coefficients indicate a combination of decaying functions over time. Therefore, the final expression represents the inverse Laplace transform of the given function.