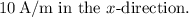Final answer:
The tangential component of the magnetic field intensity in the magnetic material close to the interface is
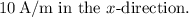
Step-by-step explanation:
To find the magnetic field intensity
 in the magnetic material (x > 0) close to the interface, we can use the boundary conditions for magnetic fields at an interface between different materials.
in the magnetic material (x > 0) close to the interface, we can use the boundary conditions for magnetic fields at an interface between different materials.
The boundary condition for the magnetic field intensity at the interface is given by:
![\[ H_(t1) - H_(t2) = K_s * \hat{n} \]](https://img.qammunity.org/2024/formulas/physics/college/3nk1hpoqhw7d879y1bt4w3p5x2zmeh7nh6.png)
where:
 and
and
 are the tangential components of
are the tangential components of
 on either side of the interface,
on either side of the interface,
 is the surface current density,
is the surface current density,
 is the unit normal vector pointing from material 1 to material 2.
is the unit normal vector pointing from material 1 to material 2.
Since there is no surface current
 , the equation simplifies to:
, the equation simplifies to:
![\[ H_(t1) = H_(t2) \]](https://img.qammunity.org/2024/formulas/physics/college/odzgvjq2fwdg6tgrsxjotwwxe5k9k5vziu.png)
Now, let's consider the given magnetic field intensity in air
![(\( x < 0 \)):\[ \mathbf{H}_{\text{air}} = 10 \, \text{A/m} \cdot \mathbf{x} + 3 \, \text{A/m} \cdot \mathbf{y} - 7 \, \text{A/m} \cdot \mathbf{z} \]](https://img.qammunity.org/2024/formulas/physics/college/ps59hqs14u10oto2rktp619bqmb6ybtnvj.png)
The tangential component in the air side
 is the component parallel to the interface, which is the
is the component parallel to the interface, which is the
 in this case:
in this case:
![\[ H_(t1) = 10 \, \text{A/m} \]](https://img.qammunity.org/2024/formulas/physics/college/mda20zipmok7an3uboeht4ogi0p6jx0lj1.png)
Now, since there is no surface current,
 . Therefore, the magnetic field intensity in the magnetic material close to the interface
. Therefore, the magnetic field intensity in the magnetic material close to the interface
 is also:
is also:
![\[ H_(t2) = 10 \, \text{A/m} \]](https://img.qammunity.org/2024/formulas/physics/college/goavsgbuvuq40eifw5fxbfx5b03hd5usd6.png)
So, the tangential component of the magnetic field intensity in the magnetic material close to the interface is