Question

3x+4=8y-3 5x+1=10y-4

Answer 1

x-3 and y=2

Explanation:

Answer 2

The solution to the system is
`\(x = 3\) and \(y = 2\).`

To solve the system of equations:

`3x + 4 &= 8y - 3 \\5x + 1 &= 10y - 4`

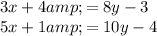
We can use either the substitution method or the elimination method. Let's use the substitution method.

1. First equation:**

`\[ 3x + 4 = 8y - 3 \]`

Isolate x by subtracting 4 from both sides:

`\[ 3x = 8y - 7 \]`

Divide both sides by 3:

`\[ x = (8y - 7)/(3) \]`

2. Substitute into the second equation:

`\[ 5 \left( (8y - 7)/(3) \right) + 1 = 10y - 4 \]`

Multiply both sides by 3 to clear the fraction:

`\[ 5(8y - 7) + 3 = 30y - 12 \]`

Distribute and combine like terms:

`\[ 40y - 35 + 3 = 30y - 12 \]`

`\[ 40y - 35 + 3 = 30y - 12 \]`

Subtract 30y from both sides:

`\[ 10y - 32 = -12 \]`

Add 32 to both sides:

`\[ 10y = 20 \]`

Divide by 10:

`\[ y = 2 \]`

3. Substitute y back into the expression for x:**

`\[ x = (8(2) - 7)/(3) \]`

`\[ x = (9)/(3) \]`

`\[ x = 3 \]`

So, the solution to the system is x = 3 and y = 2.

The following question may be like this:

Solve the equation

3x+4=8y-3

5x+1=10y-4