Question

Find all complex zeros of the polynomial function and write the polynomial in completely factored form.

f(x)=-3x⁵+23x⁴-37x³-189x²-160x-34

Answer 1

The complex zeros of the polynomial function are 5 + 3i and 5 - 3i

The factored form of the polynomial is f(x) = -(x + 1)(x + 1)(3x + 1)(x² - 10x + 34)

Finding the complex zeros of the polynomial function

From the question, we have the following parameters that can be used in our computation:

f(x) = -3x⁵ + 23x⁴ - 37x³ - 189x² - 160x - 34

Using the remainder theorem, we check if x + 1 is a factor of the polynomial

So, we have

f(-1) = -3(-1)⁵ + 23(-1)⁴ - 37(-1)³ - 189(-1)² - 160(-1) - 34

f(-1) = 0

This means that x + 1 is a factor

So, we have

-3x⁴ + 26x³ - 63x² - 126x - 34

x + 1 | -3x⁵ + 23x⁴ - 37x³ - 189x² - 160x - 34

-3x⁵ - 3x⁴

---------------------------------------------------------------------------

26x⁴ - 37x³ - 189x² - 160x - 34

26x⁴ + 26x³

---------------------------------------------------------------------------

-63x³ - 189x² - 160x - 34

- 63x³ - 63x²

---------------------------------------------------------------------------

- 126x² - 160x - 34

- 126x² - 126x

--------------------------------------------------------------

-34x - 34

This means that

-3x⁵ + 23x⁴ - 37x³ - 189x² - 160x - 34 = (x + 1)(-3x⁴ + 26x³ - 63x² - 126x - 34)

Testing if x + 1 is a factor of -3x⁴ + 26x³ - 63x² - 126x - 34 using synthetic division, we have

-1 | -3 26 - 63 -126 -34

| 3 -29 92 34

-3 29 -92 - 34 0

So, we have

-3x⁵ + 23x⁴ - 37x³ - 189x² - 160x - 34 = (x + 1)(x + 1)(-3x³ + 29x² - 92x - 34)

Using the long division again, we have

-x² + 10x - 34

3x + 1 | -3x³ + 29x² - 92x - 34

-3x³ - x²

------------------------------------------------

30x² - 92x - 34

30x² + 10x

-----------------------------------------------------

-102x - 34

-102x - 34

----------------------------------------------------------

0

So, we have

f(x) = -3x⁵ + 23x⁴ - 37x³ - 189x² - 160x - 34 = (x + 1)(x + 1)(3x + 1)(-x² + 10x - 34)

Rewrite as

f(x) = -(x + 1)(x + 1)(3x + 1)(x² - 10x + 34)

Calculating the factor of x² - 10x + 34 using the quadratic formula, we have

`x = (-b \pm √(b^2 - 4ac))/(2a)`

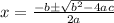
So, we have

`x = (10 \pm √((-10)^2 - 4 * 1 * 34))/(2 * 1)`

`x = (10 \pm √(-36))/(2)`

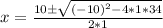
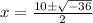
Evaluate the square root

x = (10 ± 6i)/2

So, we have

x = 5 ± 3i

This means that the complex roots are 5 + 3i and 5 - 3i