The future value of $100 monthly investments at 6.25% compounded monthly after 4 years is approximately $5,425.53.
Let's calculate the future value of the monthly investments using the formula for the future value of an ordinary annuity:
![\[ FV = P \left( ((1 + r)^(nt) - 1)/(r) \right) \]](https://img.qammunity.org/2024/formulas/mathematics/college/4z5alb4zu1qc937f1hzaihq7bh9m6cwz0b.png)
Where:
-
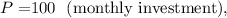
-

-
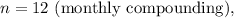
-
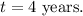
![\[ FV = 100 \left( ((1 + (0.0625)/(12))^(12 * 4) - 1)/((0.0625)/(12)) \right) \]](https://img.qammunity.org/2024/formulas/business/high-school/4ov9zsa0irkvw0aoylxa8dwr6teheyplvj.png)
After performing the calculation:
![\[ FV \approx 100 \left( ((1 + 0.005208333333)^(48) - 1)/(0.005208333333) \right) \]](https://img.qammunity.org/2024/formulas/business/high-school/ha9mtp83d5ihbpc7xv4erncuomcv3ynlop.png)
![\[ FV \approx 100 \left( ((1.005208333333)^(48) - 1)/(0.005208333333) \right) \]](https://img.qammunity.org/2024/formulas/business/high-school/q0nxhj2ovz4oqoddrrrrd6zyhy5cqly02z.png)
![\[ FV \approx 100 \left( (1.28203723108 - 1)/(0.005208333333) \right) \]](https://img.qammunity.org/2024/formulas/business/high-school/x1hmywppdrq0ymhzp8iemqy01pgnofk7jh.png)
![\[ FV \approx 100 \left( (0.28203723108)/(0.005208333333) \right) \]](https://img.qammunity.org/2024/formulas/business/high-school/2qze3054ygcbat2jj9hh8g2v90aijd1il7.png)
![\[ FV \approx 100 * 54.2552504 \]](https://img.qammunity.org/2024/formulas/business/high-school/d5cygv486t43uxy4sy3vptla4j19ko24y7.png)
![\[ FV \approx $5,425.525 \]](https://img.qammunity.org/2024/formulas/business/high-school/7ns0yvxbms2xqcc0miqh43dawl74xkw2pw.png)
Therefore, the future value of the monthly investments after 4 years at a 6.25% monthly interest rate compounded monthly is approximately $5,425.53.