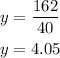Given that y is inversely proportional to x, then they satisfy the following equation:
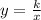
where k is the constant of proportionality.
Substituting with y = 18 and x = 9, we get:
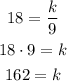
Therefore, the variation equation in terms of x is:

Substituting with x = 40, the value of y is: