Question

Find the altitude above the surface of the Moon where a "lunasynchronous" satellite would orbit. The period of

a lunar day is 27.332 days. (Rm = 1,736,482 m, Mm = 7.34767309 x 10¹2 kg)

Answer 1

The altitude above the surface of the Moon where a "lunasynchronous" satellite would orbit is 1.15328915 × 10¹⁰ m

What is a lunar synchronous satellite?

A lunar synchronous orbit is an orbit in which a satellite's orbital period corresponds to the rotation period of the Moon. In this situation, the Moon's rotation period is regarded to be 27.332 days.

Using Kepler's third law to calculate the orbital period (T) of the satellite, we have;

`T=2 \pi \sqrt{(r^3)/(GM)}`

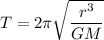
where;

• G = gravitational constant
  `(6.674 * 10^(-11) Nm^2/kg^2)`
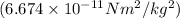
• T = orbital period 27.332 days = 2361484.8 sec
• r = average orbital radius
• M = mass of celestial body orbited 7.34767309 × 10²² kg

Let's first solve for the average orbital radius:

`r =\Big((T)/(2 \pi) \Big)^(2/3) √(GM)`

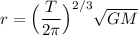
replacing the values into the equation:

`r =\Big((2361484.8)/(2 \pi) \Big)^(2/3) \sqrt{(6.674*10^(-11)) * (7.34767309* 10^(22)) \ kg}`

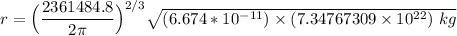
r = 1.15328915 × 10¹⁰ m

Now, the altitude (h) can be estimated by subtracting the radius of the moon from the orbital radius.

h = r - Rm

h = 1.15328915 × 10¹⁰ m - 1736482 m

h = 1.15328915 × 10¹⁰ m

Therefore, the altitude above the surface of the Moon where a "lunasynchronous" satellite would orbit is 1.15328915 × 10¹⁰ m.