Answer:
The given exponential functions f(x) and g(x) will be equal for the value of x as 4.1466.
Explanation:
We need to give exponential function to the given constraints.
since f(x) is a decreasing function so
f(x) =

where
a = Initial value
r = rate at which function is decreasing
as we are given the values of a and r such as a = 800 and r = 12%
upon substituting these values in the equation we get
f(x) =

=
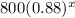
similarly we will do for g(x) but the only difference in f(x) and g(x) will be that f(x) in a decreasing exponential function whereas g(x) is an increasing function.
g(x) =

where a is initial value and r is the rate at which the function is increasing so upon substituting these values we get.
g(x) =
 =
=
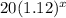
Now,
we need to find the value of x for which f(x) and g(x) will be equal.
so
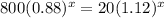
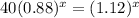
x will be approximately 4.1466
Therefore the given exponential functions f(x) and g(x) will be equal for the value of x as 4.1466.