Question

I am trying to solve for x and y. I’m just not clear on how to do this.

Answer 1

(-1, 2)

Explanation:

x-3y = -7

3x+y = -1 <===== multiply this equation by 3 to get

9x + 3y = -3 <=====add this to first equation ( this will eliminate 'x')

10x = -10 so x = -1

use this value of 'x 'in any of the equations to compute 'y'

-1 -3y = -7

-3y = -6

y = 2

Answer 2

Hello!

Let's write this system below:

`\begin{cases}x-3y=-7\text{ eq i)} \\ 3x+y=-1\text{ eq ii)}\end{cases}`

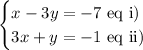
Notice that I divided it into two equations, i) and ii).

The first step: let's isolate one of the variables.

I'll isolate the variable X in equation i), look:

`\begin{gathered} x-3y=-7 \\ x=-7+3y \end{gathered}`

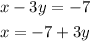
From now on, we will use this value when referring to X.

Second step: in the other equation, we will replace the variable with the obtained value.

So, let's replace where's X in equation ii) by (-7 +3y):

`\begin{gathered} 3x+y=-1 \\ 3\cdot(-7+3y)+y=-1 \\ -21+9y+y=-1 \\ -21+10y=-1 \\ 10y=-1+21 \\ 10y=20 \\ y=(20)/(10) \\ \\ y=2 \end{gathered}`

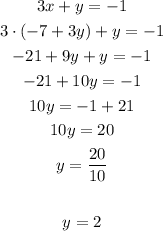
At this moment we know the value of the variable Y as 2. So, we can choose any of the equations and replace this value.

Let's replace Y in the first equation now:

`\begin{gathered} x-3y=-7 \\ x-3\cdot(2)=-7 \\ x-6=-7 \\ x=-7+6 \\ x=-1 \end{gathered}`

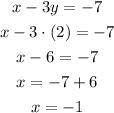
So, the solution of this system is x = -1 and y = 2.