Question

Total world consumption of iron was approximately 900 million tons in 1993. If consumption had increased by 2.5% each year and the resources available for mining in 1993 were 450 billion tons, how much longer would the world’s iron resources have lasted?

Answer 1

Explanation:

We can model the annual consumption of iron by the equation

c = 900 million tons x
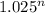`1.025^n`, where

n is the number of years after 1993 and

c is the consumption for that year.

An estimate for the total consumption of iron can now be obtained by integrating this equation with respect to a dummy variable, x from 0 to n.

`C = 900*10^6* \int\limits^n_0 {1.025^x} \, dx`

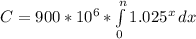
This equation simplifies to

C = 900 million tons x (1.025^n - 1) / ln(1.025), where

x is a dummy variable and

C is the total consumption of iron n years after 1993.

Let R be the amount of iron remaining at n years after 1993, so

R = 480 billion tons - C

R = 480 billion tons - 900 million tons x (1.025^n - 1) / ln(1.025)

We need to find the value of n when R is 0, so

0 = 480 billion tons - 900 million tons x (1.025^n - 1) / ln(1.025)

Simplify this equation to obtain

n = 107.4

So the iron will run out in the year 1993 + 107 = 2100