Question

You have enough tickets to play 6 different gamesat the amusement park. If there are 14 games,how many ways can you choose six ?1111How many different ways can 9 trumpet playersin the marching band line up?+---1-Seven students worked together on a project.How many ways can their teacher choose four topresent the project?+-There are 18 offensive players on the hockeyteam. How many ways can the coach choose a ||left wing, center, and right wing to start the game,1-11How many different 12-letter arrangements canbe made using the letters in the wordINDIANAPOLIS+1There are 26 gold fish in the tank at the store. Howmany ways can Ben choose five?C.11

Answer 1

the This problem uses permutation and combination. The formula to find the permutation is

`P(n,r)=(n!)/((n-r)!)`

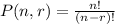
while the formula to find the combination is

`C(n,r)=(n!)/(r!(n-r)!)`

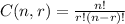
We need to know what type of problem the given is so that we can choose what equations we will be using on the equation above.

7. This problem is a combination problem since we want to know the total combinations of games that are possible for n = 14 and you have r = 6. The total combination is

`C(n,r)_{}=(14!)/(6!(14-6)!)=3003`

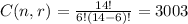
Hence, there are 3003 ways you can choose six games.

8. We want to know how many ways a trumpet player can be arranged in a marching band lineup. We have n = 0 while our r here is also equal to 9 because we are arranging all the trumpet players in a different manner. Hence, using the permutation equation, we have

`P(n,r)=\frac{9!}{(9-9)!_{}}=362880`

Hence, they can be arranged 362880 times.

9. This problem is a combination problem since we want to know how many possible arrangements can be done if a group that composed of n = 7, we arranged r = 4. Hence, using a combination equation, we have

`C(n,r)_{}=(7!)/(4!(7-4)!)=35`

Hence, they can be arranged in 35 ways.

10. Since we are dealing with arrangements, this is a permutation problem. We have n = 18 and we will arrange them in r = 3 ways. Hence, the total number of permutations possible is

`P(n,r)=\frac{18!}{(18-3)!_{}}=4896`

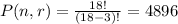
Hence, they can be arranged in 4896 ways.

11. There are 12 letters present in the word INDIANAPOLIS. Since there are repetitions of letters, we will consider those. We have 3 I's, 2 A's, 2 N's. The possible permutation for the distinct arrangement of letters for INDIANAPOLIS can be computed as

`P(n,r)=(12!)/((3!)(2!)(2!))=19958400_{}`

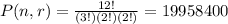
The word INDIANAPOLIS can be arranged 19958400 without repetition of letters in the same placement.

12. This problem is a combination problem. We have n = 26 goldfishes and Ben wants to choose r = 5. Using the combination equation, we have