Question

Use a graphing utility to complete the table and estimate the limit as x approaches infinity. Then use a graphing utility to graph the function and estimate the limit. Finally, find the limit analytically and compare your results with the estimates. (Round your answers in the table to three decimal places.)

Answer 1

we have the function

`f(x)=\frac{x+1}{x\sqrt[]{x}}`

Complete the table

Substitute each value of x in the given function to obtain the value of f(x0

so

For x=10^0=1

`f(x)=\frac{1+1}{1\sqrt[]{1}}=2`

For x=10^1=10

`f(x)=\frac{10+1}{10\sqrt[]{10}}=0.348`

For x=10^2=100

`f(x)=\frac{100+1}{100\sqrt[]{100}}=0.101`

For x=10^3=1,000

`f(x)=\frac{1000+1}{1000\sqrt[]{1000}}=0.032`

For x=10^4=10,000

`f(x)=\frac{10000+1}{10000\sqrt[]{10000}}=0.010`

For x=10^5=100,000

`f(x)=\frac{100000+1}{100000\sqrt[]{100000}}=0.003`

For x=10^6=1,000,000

`f(x)=\frac{1000000+1}{1000000\sqrt[]{1000000}}=0.001`

therefore

`\lim _(x\to\infty)f(x)=0`

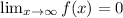
see the attached figure below

as the value of x increases -----> the value of f(x) decreases

as x ----> ∞ f(x) ---> 0