Question

Find x in triangle ABC using geometric means.​

Answer 1

Given:

The figure of a right angle triangle.

To find:

The value of x using geometric mean.

Solution:

According to the geometric mean altitude theorem, if an altitude h divides the hypotenuse in two parts a and b, then

`(a)/(h)=(h)/(b)`

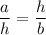
Let attitude from A touches the hypotenuse at point D.

Using this in the given triangle, we get

`(BD)/(AD)=(AD)/(CD)`

`(12)/(x)=(x)/(3)`

`12* 3=x^2`

`36=x^2`

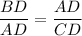
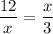
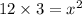
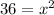
Taking square root on both sides, we get

`\pm √(36)=x`

`\pm 6=x`

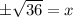
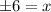
Side cannot be negative. Therefore, the only value of x is 6.