Question

a solid metal cone with radius of base 12 cm and height 24 cm is melted to form spherical solid balls of diameter 6 cm each. Find the number of the balls thus formed​

Answer 1

32 solid balls are formed.

Explanation:

Let suppose that volume of the cone is equal to the total volume of balls, of which we derive the following formula:

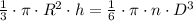`(1)/(3)\cdot \pi\cdot R^(2)\cdot h = (1)/(6)\cdot \pi \cdot n \cdot D^(3)` (1)

Where:

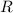`R` - Radius of the base of cone, measured in centimeters.

`h` - Height of cone, measured in centimeters.

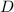`D` - Diameter of sphere, measured in centimeters.

`n` - Number of balls, no unit.

Then, we clear the number of balls:

`2\cdot R^(2)\cdot h = n\cdot D^(3)`

`n = (2\cdot R^(2)\cdot h)/(D^(3))`

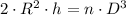
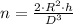
If we know that
`R = 12\,cm`,
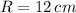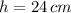`h = 24\,cm` and
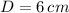`D = 6\,cm`, then the number of balls is:

`n = (2\cdot (12\,cm)^(2)\cdot (24\,cm))/((6\,cm)^(3))`

`n = 32`

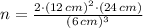
32 solid balls are formed.