1 Answer

Ask a Question

Vbali · Answer 1 · 2023-06-01T09:13:56+0000

Step 1: Write out the Z score formula

$\begin{gathered} Z=(x-\mu)/(\sigma) \\ x=\text{score} \\ \mu=\operatorname{mean} \\ \sigma=s\tan dard\text{ deviation} \end{gathered}$

Step 2: Calculate the z scores for the two values ( 75 and 80 )

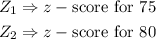
$\begin{gathered} Z_1\Rightarrow z-\text{score for 75} \\ Z_2\Rightarrow z-\text{score for 80} \end{gathered}$
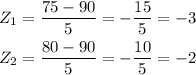
$\begin{gathered} Z_1=(75-90)/(5)=-(15)/(5)=-3 \\ Z_2=(80-90)/(5)=-(10)/(5)=-2 \end{gathered}$

The probability that the mean is between 75 and 80 will be

[tex]Pr(-3Thus, the probability will be[tex]\begin{gathered} Pr(-3Hence, the indicated probability P(75

Assume the random variable x is normally distributed with mean y = 90 and standard-example-1

0 Comments

Your comment on this question:

Your answer

1 Answer

0 Comments

Your comment on this answer:

Other Questions