1 Answer

Donparalias · Answer 1 · 2022-11-26T23:35:20+0000

Given:

The functions are:

(1)
h(x)=√(1-x)

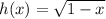
(2)
x+y=4

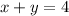
(3)
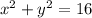
x^2+y^2=16

To find:

The domain of given functions.

Solution:

Domain is the set of input and x -values.

Value under the square root must be positive because if the number under square root is negative, then it is a complex or imaginary number.

(1)
h(x)=√(1-x)

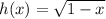
The function is defined if

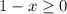
$1-x\geq 0$

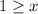
$1\geq x$

The function is defined for all real values of x which are less than or equal to 1.

Therefore, the domain of the function is (-∞,1].

(2)
x+y=4

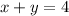
It is a linear function and linear function is defined for all real values of x.

Therefore, the domain of the function is (-∞,∞).

(3)
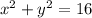
x^2+y^2=16

It can be written as

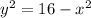
y^2=16-x^2

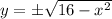
$y=\pm √(16-x^2)$

It is defined if

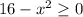
$16-x^2\geq 0$

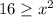
$16\geq x^2$

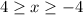
$4\geq x\geq -4$

This function defined for all real values of x from -4 to 4.

Therefore, the domain of the function is [-4,4].

Please log in or register to add a comment.