Answer:
The second line cuts the x-axis at x = -5/2.
Explanation:
The given line:
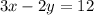
Intersects a second line at x = 2.
This second line is perpendicular to the first.
And we want to find the second line's x-intercept.
First, rearrange the first line into slope intercept form:

So:
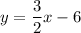
We can see that the slope of the first line is 3/2.
It intersects the second line at x = 2.
So, the y-value of both the first and second line at x = 2 is the same.
Find the y-value by using the first line:
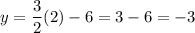
So, a point on both lines is (2, -3).
Since the second line is perpendicular to the first, its slope it the first's negative reciprocal.
The negative reciprocal of 3/2 is -2/3.
So, the slope of the second line is -2/3.
And we determined that it passes through (2, -3).
Then by the point-slope form:
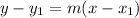
Substitute:

Distribute:
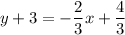
So:
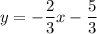
The second line will cut the x-axis when y = 0.
So:

Multiply both sides by -3:
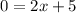
Solve for x:
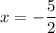
The second line cuts the x-axis at x = -5/2.