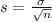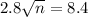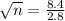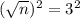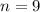Question

Given a population mean of 27.1 with a standard deviation of 8.4 and a sample size of 10, answer these questions.

part A: what is the standard deviation of the sampling distribution of x hat? show your work.
PartB: what does the sample size need to be if you want the standard deviation of the sampling distribution of x hat to be 2.8? show your work.

Answer 1

a) 2.66

b) 9

Explanation:

Central Limit Theorem

The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean
`\mu` and standard deviation
`\sigma`, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
`\mu` and standard deviation
`s = (\sigma)/(√(n))`.

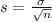part A: what is the standard deviation of the sampling distribution of x hat? show your work.

We have that
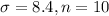`\sigma = 8.4, n = 10`. So

`s = (\sigma)/(√(n)) = (8.4)/(√(10)) = 2.66`

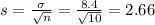
PartB: what does the sample size need to be if you want the standard deviation of the sampling distribution of x hat to be 2.8?

This is n when
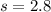`s = 2.8`. So

`s = (\sigma)/(√(n))`

`2.8 = (8.4)/(√(n))`

`2.8√(n) = 8.4`

`√(n) = (8.4)/(2.8)`

`√(n) = 3`

`(√(n))^2 = 3^2`

`n = 9`