Question

`g(x)= (x^2+3x+2)/(x^2+x-2)`

Please find the following using algebraic analysis.

a. Find the holes in this function’s graph:

b. Find the function’s vertical asymptotes:

c. Find the function’s horizontal asymptotes:

d. Find the y-intercept of g(x):

e. Find the x-intercepts of g(x):

f. Draw a graph of g(x) − :

Answer 1

The hole in the function’s graph is x = -2

The function’s vertical asymptotes is x = 1

The function’s horizontal asymptotes is y = 1

The y-intercept of g(x) is (0, -1)

The x-intercept of g(x) is (-1, 0)

Finding the holes in the function’s graph

From the question, we have the following parameters that can be used in our computation:

`\text{g(x)} = (x^2 + 3x + 2)/(x^2 + x - 2)`

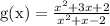
Factorize the expression

So, we have

`\text{g(x)} = ((x + 2)(x +1))/((x + 2)(x - 1))`

The common factor in the numerator and the denominator is x + 2

So, we have

x + 2 = 0

x = -2

This means that the hole in the function’s graph is x = -2

Finding the function’s vertical asymptotes

Here, we have

`\text{g(x)} = ((x + 2)(x +1))/((x + 2)(x - 1))`

This gives

`\text{g(x)} = (x +1)/(x - 1)`

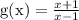
Set the denominator to 0

x - 1 = 0

Evaluate

x = 1

So, the function’s vertical asymptotes is x = 1

Finding the function’s horizontal asymptotes

We have

`\text{g(x)} = (x +1)/(x - 1)`

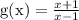
The quotient of the leading coefficients of the numerator and the denominator is the horizontal asymptote

So, we have

y = 1/1

y = 1

So, the function’s horizontal asymptotes is y = 1

Finding the y-intercept of g(x)

Here, we set x = 0

So, we have

`\text{g(0)} = (0 +1)/(0 - 1)`

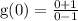
Evaluate

g(0) = -1

So, the y-intercept of g(x) is (0, -1)

Finding the x-intercept of g(x)

Here, we set y = 0

So, we have

`(x +1)/(x - 1)=0`

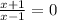
Evaluate

x + 1 = 0

x = -1

So, the x-intercept of g(x) is (-1, 0)

The graph of the function is attached