Question

A population of 2000 fish increases at an annual rate of 7.5%. Write the model, then predict how

many fish will there be in 10 years?

Answer 1

The model is
`P(t) = 2000(1.075)^(t)`.

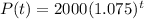There will be 4122 fish in 10 years.

Explanation:

Exponentially increasing population:

An exponentially increasing population can be represented by the following model:

`P(t) = P(0)(1+r)^t`

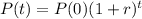
In which P(t) is the population after t years, P(0) is the initial population, and r is the growth rate, as a decimal.

A population of 2000 fish increases at an annual rate of 7.5%.

This means that
`P(0) = 2000, r = 0.075`

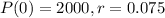
So

`P(t) = P(0)(1+r)^t`

`P(t) = 2000(1+0.075)^t`

`P(t) = 2000(1.075)^(t)`

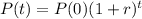
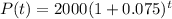
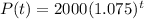
This is the model.

How many fish will there be in 10 years?

This is P(10).

`P(t) = 2000(1.075)^(t)`

`P(10) = 2000(1.075)^(10) = 4122`

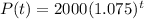
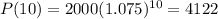
There will be 4122 fish in 10 years.