Question

Are the triangles similar? if so what is the scale factor?

Answer 1

a) Yes, The scale factor is 3/2

Step-by-step explanation

Step 1

to check if the triangles are similar, we need to prove that the ratios of the longest side and one sideof the triangle are similar

so

let

`ratio=\frac{longest\text{ side}}{side}`

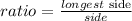
hence

`\begin{gathered} ratio_1=(8)/(5)=1.6 \\ ratio_2=(12)/(7.5)=1.6 \end{gathered}`

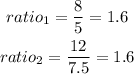
therefore, the triangles are similar

Step 2

now, to find the scale factor we use the formula

`scale\text{ factor =}\frac{final\text{ length }}{original\text{ length}}`

so, let's take the longest side on each triangle

`\begin{gathered} final\text{ length=12} \\ original\text{ length=8} \end{gathered}`

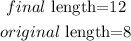
replace and calculate

`\begin{gathered} scale\text{ factor =}\frac{final\text{ length }}{original\text{ length}} \\ scale\text{ factor =}(12)/(8)=(3)/(2) \end{gathered}`

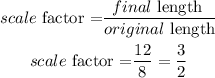
therefore, the answer is

a) Yes, The scale factor is 3/2

I hope this helps you