Question

The half-life of tungsten 188 is 69.4 days. Initially, there are 0.725 kg of this isotope. How much of the isotope will remain after 147 days?(a) 0.104 kg(b) 0.167 kg(c) 0.237 kg(d) 0.255 kg

Answer 1

In order to determine the amount of tungsten after 147 days, use the following formula for the radioactive decay:

`A=A_oe^(-\lambda t)`

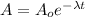
where

A: amount of tungsten after t days

Ao: initial amount of tungsten = 0.725 kg

t: time = 147 days

λ: decay constant

Then, it is necessary to find the value of λ. Use the following formula:

`\lambda=\frac{\ln 2}{t_{(1)/(2)}}`

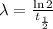
where t1/2 is the half-life of tungsten (69.4 days)

`\lambda=(\ln 2)/(69.4)=0.00998`

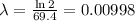
next, replace the previous result and the values of the other parameters into the formula for A:

Hence, after 147 days, there are 0.167 kg of tungsten 188