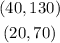Question

The equations in the red box I need to use substitution. Explaining the steps as I go.

Answer 1

We are given the following system of equations:

`\begin{gathered} y=-x^2+63x-790,(1) \\ y=3x+10,(2) \end{gathered}`

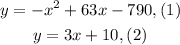
We will substitute the value of "y" from the first equation into the second equation:

`-x^2+63x-790=3x+10`

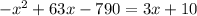
Now we subtract "3x" from both sides:

`-x^2+63x-3x-790=10`

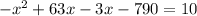
Adding like terms:

`-x^2+60x-790=10`

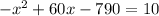
Now we subtract 10 from both sides:

`-x^2+60x-790-10=0`

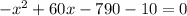
Adding like terms:

`-x^2+60x-800=0`

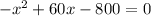
Now we multiply by -1 on both sides of the equation:

`x^2-60x+800=0`

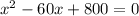
Now we factor in the left side. We need two numbers that when multiplied the product is 800 and their algebraic sum is -60. Those numbers are -40 and -20. Therefore, we get:

`(x-40)(x-20)=0`

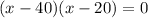
Now we set each factor to zero:

`\begin{gathered} x-40=0 \\ x=40 \end{gathered}`

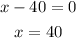
For the next factor:

`\begin{gathered} x-20=0 \\ x=20 \end{gathered}`

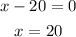
These are the two values of "x" for the solution. To get the corresponding value of "y" we substitute in the second equation. Substituting the first value we get:

`\begin{gathered} y=3(40)+10 \\ y=120+10 \\ y=130 \end{gathered}`

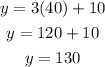
Now we substitute the second value:

`\begin{gathered} y=3(20)+10 \\ y=60+10 \\ y=70 \end{gathered}`

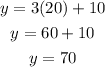
Therefore, the solutions of the system are:

`\begin{gathered} (40,130) \\ (20,70) \end{gathered}`