Answer:
1) x = 8 cm
2) x = 7m
3) x = 14 m
4) x = 1.875 in
Explanation:
In order to find the value of x, we can use the Total surface area of the cuboid formula:
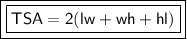
where
TSA = Total surface area
l = length of the cuboid
w = width of the cuboid
h = height of the cuboid
1)
Let's determine the value of x in the cuboid.
We are given that the surface area of the cuboid is 152 cm², the width is 2 cm, and the height is 6 cm. We need to find the length, which is represented by x.
We can set up an equation to represent the surface area of the cuboid:
2(wh + lh + wl)= 152
2wh + 2lh + 2wl = 152
Substituting the given values, we get:
2(2)(6) + 2(6)(x) + 2(2)(x) = 152
24 + 12x + 4x = 152
Combining like terms, we get:
16x +24 = 152
Subtracting 24 on both sides:
16x +24 = 152 - 24
16x = 128
Dividing both sides by 16, we get:
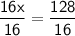
x = 8 cm
Therefore, the length of the cuboid is 8 cm.
2)
To find the value of x, we need to use the formula for the surface area of a cuboid. This formula is:
2(lw + wh + hl) = 166
We are given that the width (w) is 4 m, the height (h) is x m, and the length (l) is 5 m. We are also given that the surface area (S) is 166 m².
Substituting the given values into the formula, we get:
2(4x + 5x + 20) = 166
Combining like terms, we get:
2(9x + 20) = 166
18x + 40 = 166
Subtract both sides by 40.
18x + 40 - 40= 166 - 40
18x = 126
Dividing both sides by 18, we get:
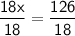
x = 7
Therefore, the value of x is 7 m.
3)
To determine the value of x in the cuboid, we can use the formula for the surface area of a cuboid:
2(lw + wh + hl) = 292
We are given that the width (w) is 4 m, the height (h) is 5 m, and the length (l) is x m. We are also given that the surface area (S) is 292 m².
Substituting the given values into the formula, we get:
2(4x + 5x + 20) = 292
Combining like terms, we get:
2(9x + 20) = 292
18x + 40 = 292
Subtract 40 on both sides:
18x + 40 - 40 = 292 - 40
18x = 252
Dividing both sides by 18, we get:
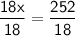
x = 14
Therefore, the value of x is 14 m.
4)
Given the surface area of 31.25 in², width of 2.5 in², height of x , and length represented by 2.5in, we can use the formula for the surface area of a cuboid to find the value of x.
Substituting the given values into the formula, we get:
2(2.5x + 2.5x + 2.5(2.5)) = 31.25
Combining like terms, we get:
2(5x + 6.25) = 31.25
10x + 12.5 = 31.25
Subtracting 12.5 from both sides, we get:
10x + 12.5 - 12.5 = 31.25 - 12.5
10x = 18.75
Dividing both sides by 10, we get:

x = 1.875 in
Therefore, the value of x is 1.875 in.