Question

Solve the right triangle. Round decimal answers to the nearest tenth. find RSfind RTfind angle T

Answer 1

Δ RST shown in the picture is a right triangle, we know the measure of ∠R and ∠S, and the length of side ST.

To determine the length of the missing angle, you have to remember that the sum of the inner angles of a triangle add up to 180º

Then we can calculate the measure of ∠T as follows:

`\begin{gathered} \angle R+\angle S+\angle T=180 \\ 57+90+\angle T=180 \\ 174+\angle T=180 \\ \angle T=180-174 \\ \angle T=33º \end{gathered}`

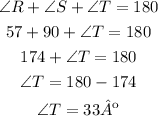
The measure of the missing angle is ∠T=33º

To determine the lengths of the missing sides RS and RT, you have to use the trigonometric ratios of sine, cosine, and tangent. These ratios are defined as follows:

`\begin{gathered} \sin \theta=(opposite)/(hypothenuse) \\ \cos \theta=(adjacent)/(hypothenuse) \\ \tan \theta=(opposite)/(adjacent) \end{gathered}`

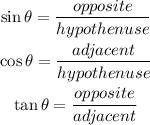
"θ" represents the angle of interest.

Using ∠R as a point of reference, side ST is across this angle so it is the side of the triangle "opposite" to it.

Side RS is next to ∠R, so it is the side "adjacent" to it.

The trigonometric ratio that shows the relationship between the opposite and adjacent sides to an angle is the tangent. Using the definition of the tangent you can determine the length of RS as follows:

`\tan R=(RS)/(ST)`

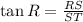
-First, write the expression for RS, which means that you have to pass "ST" to the left side of the equal sign by applying the opposite operation to both sides of it.

`\begin{gathered} ST\tan R=ST\cdot(RS)/(ST) \\ ST\tan R=RS \end{gathered}`

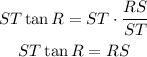
-Replace the expression with the values of ∠R and ST:

`\begin{gathered} 15\cdot tan57=RS \\ 23.09=RS \\ RS\approx23.1 \end{gathered}`

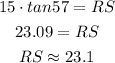
Side RS measures 23.1

Side RT is the longest side of the triangle, and thus, its hypothenuse. To determine its length using ∠R and side ST, you have to apply the definition of the sine:

`\sin R=(ST)/(RT)`

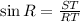
-Pass the term RT to the other side of the equation to take the term out of the denominators place:

`\begin{gathered} RT\cdot\sin R=RT(ST)/(RT) \\ RT\cdot\sin R=ST \end{gathered}`

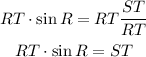
-Next, divide both sides by the sine of R to write the expression for RT

`\begin{gathered} RT\cdot(\sin R)/(\sin R)=(ST)/(\sin R) \\ RT=(ST)/(\sin R) \end{gathered}`

-Now replace the expression with the values of ∠R and ST to determine the length of RT

`\begin{gathered} RT=(15)/(\sin 57) \\ RT=12.58 \\ RT\approx12.6 \end{gathered}`

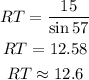
Side RT measures 12.6