Answer:
The angle of refraction measured from the normal is approximately 28.13°
Step-by-step explanation:
The angle of refraction is the angle made by the refracted ray and the normal line drawn at the point where the ray passes through the interface of the two mediums
According to Snell's law, we have;
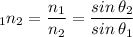
n₁·sin (θ₁) = n₂·sin(θ₂)
Where;
₁n₂ = The refractive index of air to glass = 1.5
n₁ = The refractive index of air = 1
n₂ = The refractive index of glass ≈ 1.5
θ₁ = The angle of incidence = 45°
θ₂ = The angle of refraction measured from the normal
Therefore, we have;
1/1.5 = sin(θ₂)/sin(45°)
sin(θ₂) = sin(45°)/1.5 = (√2)/2/(3/2) = (√2)/3
∴ θ₂ = arcsin((√2)/3) ≈ 28.13°
The angle of refraction measured from the normal = θ₂ ≈ 28.13°.