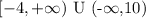Question:
Solution:
Consider the following inequalities system :
Inequality 1:
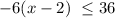
or
Inequality 2:
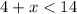
Applying the distributive property in inequality 1, we obtain:
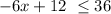
this is equivalent to:
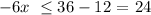
that is:
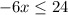
this is equivalent to:
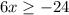
solving for x, we get:
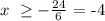
that is:
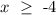
Then inequality 1 is equivalent to the following solution
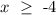
On the other hand, for inequality 2 solving for x, we get:

that is:
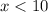
so that, the solution to the inequality system is
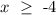
or
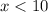
now, this is equivalent to say:
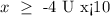
or in interval notation: