Given:
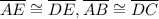
To prove:
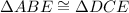
Solution:
In triangle AED,
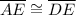
Two sides of triangle AED are equal, it means triangle AED is an isosceles triangle. The base angles of an isosceles triangle are equal. So,
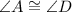
In triangle ABE and triangle DCE,
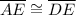 (Given)
(Given)
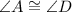 (Base angles of an isosceles triangle are equal)
(Base angles of an isosceles triangle are equal)
 (Given)
(Given)
Two corresponding sides and their included angles are congruent. So, triangles are congruent by SAS postulate of congruence.
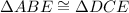 (By SAS postulate of congruence)
(By SAS postulate of congruence)
Hence proved.