Let's draw the scenario to better understand the details.
To be able to determine the height of the flagpole, let's create two different triangles with 29.5° and 39° 45' angle. The two triangles have one common base at 80 Feet, yet have different heights at H+h and H respectively.
Where,
H = Height of the library
h = Height of the flag
The two triangles are proportional at a common base, thus, let's generate this expression using the Law of Sines:
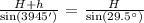
Let's simplify,
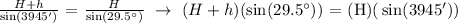
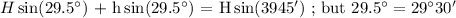
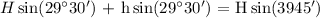
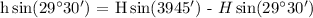
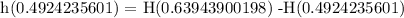
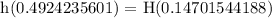
![undefined]()