Given the data set (ages of grandparents):
52, 54, 57, 61, 56, 61, 67, 64, 63, 57, 60, 50
Let's create a five-number summary that represents the given data set and also create a box plot.
A) A five number summary of a data set consists of the following:
• Minimum value
,
• First quartile
,
• Median
,
• Third quartile
,
• Maximum value
Let's determine the five-number summary of the given data set.
• Minimum value:
The minimum value is the smallest number from the given data set.
Thus, the minimum is = 50
• First quartile:
The first quartile is also called the lower quartile. It is the median of the lower half of the data set.
To find the first quartile, list out the lower half of the data set after arranging the data in acsending order.
Arrange in ascending order: 50, 52, 54, 56, 57, 57, 60, 61, 61, 63, 64, 67
Lower half: 50, 52, 54, 56, 57, 57
Median of lower half:
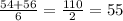
Therefore, the first quartile is = 55
• Median:
Median is the middle term of the data set.
50, 52, 54, 56, 57, 57, 60, 61, 61, 63, 64, 67
The middle terms are = 57 and 60
To find the median, divide the sum of the middle terms by 2.
Thus, we have:
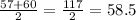
Therefore, the median of the data set is 58.5
• Third Quartile:
The third quartile is also called the upper quartile. It is the median of the upper half of the data set.
Upper half of data set = 60, 61, 61, 63, 64, 67
Median of upper half =

Therefore, the third quartile is 62
• Maximum value:
The maximum value is the greatest number in the given data set.
The greatest number in the data set is 67.
Therefore, the maximum value is 67.
We have the five-number summary that represents the data set below:
• Minimum = 50
,
• First quartile = 55
,
• Median = 58.5
,
• Third quartile = 62
,
• Maximum = 67
b) Let's create a box plot that represents the data set.
We have the box plot below: